债券凸性

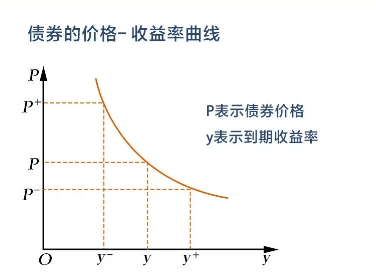
　　“凸性”（Convexity）是债券价格-收益率曲线的曲率。凸性意味着债券价格-收益曲线的斜率随着收益率而变化。

概念提出

　　债券的凸性是1984年斯坦利迪勒（Stanley Diller）提出的概念，是对债券价格曲线弯曲程度的一种度量。严格地讲，凸性是指债券到期收益率发生变动而引起的债券价格变动幅度的变动程度。凸性是债券价格对收益率的二阶导数。凸性越大，债券价格曲线弯曲程度越大，用修正久期度量债券的利率风险所产生的误差越大。凸性也是债券久期对利率敏感性的测量。在价格-收益率出现大幅度变动时，它们的波动幅度呈非线性关系。由久期做出的预测将有所偏离。凸性就是对这个偏离的修正。

公式

　　凸性反映的是债券的价格对利率的二阶敏感度，体现的是到期收益率的波动对债券价格的影响程度。计算公式如下：

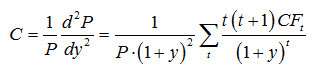
　　一般来说，债券的凸性可从资讯数据中获取，如为银行间债券，则优先取中债推荐估价凸性，其次取中证估价凸性，最后取系统模型计算的凸性；如为交易所债券，则优先取中证估价凸性，其次取中债估价凸性，最后取系统模型计算的凸性。

　　上述凸性的计算公式仅适用于固定利率债券，对于浮动利率或含权债，需要根据公式来计算有效凸性。计算公式如下：

　　组合的凸性和有效凸性为债券的凸性加权计算得到：

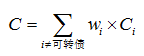
性质

　　与久期相似，债券的凸性变化，也是由债券的一些基本元素决定的，它们有：

　　期限（Maturity）：更长的期限意味着更大的凸性；

　　息票利率（Coupon Rate）：更大的息票利率意味着更大的凸性；

　　收益率（YTM）：更低的收益率意味着更大的凸性。

　　散度（Dispersion）：更为分散到整个债券寿命中的多次付款行为，意味着更大的凸性。

特征

　　（1）凸性随久期的增加而增加。若收益率、久期不变，票面利率越大，凸性越大。

　　（2）对于没有隐含期权的债券来说，凸性总大于0，即利率下降，债券价格将以加速度上升；当利率上升时，债券价格以减速度下降。

　　（3）含有隐含期权的债券的凸性一般为负，即价格随着利率的下降以减速度上升，或债券的有效持续期随利率的下降而缩短，随利率的上升而延长。因为利率下降时买入期权的可能性增加了。