考研.数学 线性代数总结2
线性代数部分―矩阵理论
一、矩阵基本概念
1、矩阵的定义―形如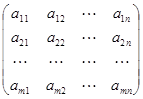 ,称为矩阵
,称为矩阵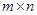 ,记为
,记为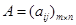 。
。
特殊矩阵有
(1)零矩阵―所有元素皆为零的矩阵称为零矩阵。
(2)方阵―行数和列数都相等的矩阵称为方阵。
(3)单位矩阵―主对角线上元素皆为1其余元素皆为零的矩阵称为单位矩阵。
(4)对称矩阵―元素关于主对角线成轴对称的矩阵称为对称矩阵。
2、同型矩阵―行数和列数相同的矩阵称为同型矩阵。若两个矩阵同型且对应元素相同,称两个矩阵相等。
3、矩阵运算
(1)矩阵加、减法:
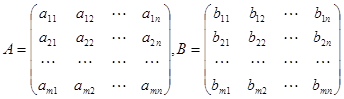 ,则
,则
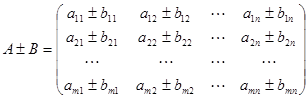 。
。
(2)数与矩阵之积:
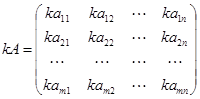 。
。
(3)矩阵与矩阵之积:
设 ,则
,则
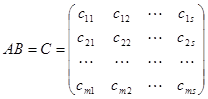 ,
,
其中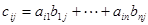 (
(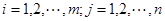 )
)
【注解】
(1)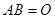 不一定有
不一定有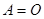 或
或 。
。
(2)矩阵乘法没有交换律。
(3)含方阵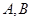 的矩阵多项式可象普通多项式一样因式分解的充分必要条件是
的矩阵多项式可象普通多项式一样因式分解的充分必要条件是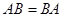 。
。
(4)设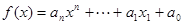 ,则定义
,则定义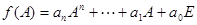 ,且关于矩阵
,且关于矩阵 的矩阵多项式可因式分解。
的矩阵多项式可因式分解。
二、方程组的矩阵形式及解的概况
方程组的基本形式为
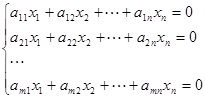 (1)
(1)
称(1)为齐次线性方程组。
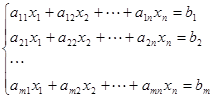 (2)
(2)
称(2)为非齐线性方程组。
令 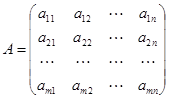 ,
, ,
, ,则(1)、(2)可分别表示为矩阵形式:
,则(1)、(2)可分别表示为矩阵形式:
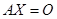 (1)
(1)
及
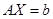 (2)
(2)
对方程组(1):
【例题1】讨论方程组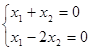 解的情况,并分析原因。
解的情况,并分析原因。
【例题2】讨论方程组 解的情况,并分析原因。
解的情况,并分析原因。
对方程组(2):
【例题1】讨论方程组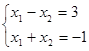 解的情况,并分析原因。
解的情况,并分析原因。
【例题2】讨论方程组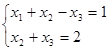 解的情况,并分析原因。
解的情况,并分析原因。
【例题3】讨论方程组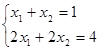 解的情况,并分析原因。
解的情况,并分析原因。
三、矩阵问题的产生
初一数学问题:解一元一次方程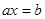
情形一:当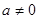 时,
时,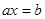 两边同时乘以
两边同时乘以 得
得 ,于是
,于是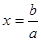 ;
;
情形二:当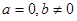 时,方程
时,方程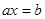 无解;
无解;
情形三:当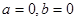 时,方程
时,方程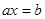 有无数个解。
有无数个解。
线性方程组的类似问题:讨论方程组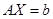 的解
的解
情形一: 是
是 阶方阵,且存在
阶方阵,且存在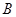 ,使得
,使得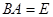
由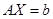 两边左乘
两边左乘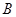 得
得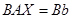 ,于是
,于是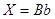 ;
;
情形二: 虽然是
虽然是 阶矩阵,但不存在
阶矩阵,但不存在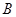 ,使得
,使得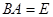
方程组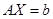 是否有解及解的情况;
是否有解及解的情况;
情形三: 是
是 矩阵,且
矩阵,且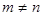
方程组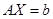 是否有解及解的情况。
是否有解及解的情况。
【注解】
(1)第一种解的情况产生矩阵的第一个核心问题―矩阵的逆阵。
(2)第二、三两种情形产生矩阵的另一个核心问题―矩阵的秩。
四、矩阵两大核心为题
(一)逆阵
1、定义―设 为
为 阶矩阵,若存在
阶矩阵,若存在 阶矩阵
阶矩阵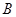 ,使得
,使得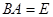 ,则称
,则称 为可逆矩阵,
为可逆矩阵,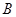 称为
称为 的逆矩阵,记为
的逆矩阵,记为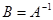 。
。
2、两个问题
【问题1】 给定一个 阶矩阵
阶矩阵 ,是否存在可逆矩阵(事实上不存在可逆矩阵的矩阵大量存在)?
,是否存在可逆矩阵(事实上不存在可逆矩阵的矩阵大量存在)?
【问题2】 若 阶矩阵
阶矩阵 可逆(即逆矩阵存在),如何求其逆矩阵?
可逆(即逆矩阵存在),如何求其逆矩阵?
3、矩阵可逆充分必要条件
定理设 为
为 阶矩阵,则
阶矩阵,则 可逆的充分必要条件是
可逆的充分必要条件是 。
。
4、求矩阵逆阵的方法
方法一:伴随矩阵法(略)
方法二:初等变换法
第一步 方程组的三种同解变形
(1)对调两个方程的位置方程组的解不变;
(2)某个方程两边同乘以一个非零常数方程组的解不变;
(3)某个方程的倍数加到另一个方程方程组的解不变。
第二步 矩阵的三种初等行变换
(1)对调矩阵的两行;
(2)矩阵的某行同乘以一个非零常数;
(3)矩阵某行的倍数加到另一行。
第三步 三种初等矩阵
(1)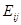 ―单位矩阵的
―单位矩阵的 行与
行与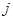 行对调或者
行对调或者 列与
列与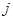 列对调所得的矩阵。
列对调所得的矩阵。
性质:1)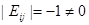 ; 2)
; 2)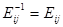 或者
或者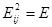 ;
;
3) 为将
为将 的
的 行与
行与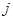 行对调所得的矩阵,
行对调所得的矩阵,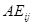 为将
为将 的
的 列与
列与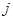 列对调所得的矩阵。
列对调所得的矩阵。
(2)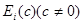 ―单位矩阵的
―单位矩阵的 行乘以
行乘以 或单位矩阵的
或单位矩阵的 列乘以
列乘以 。
。
性质:1) ; 2)
; 2) ;
;
3)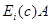 为将
为将 的
的 行乘以非零常数
行乘以非零常数 所得到的矩阵,
所得到的矩阵,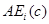 为将
为将 的
的 列乘以非零常数
列乘以非零常数 所得到的矩阵。
所得到的矩阵。
(3)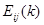 ―单位矩阵的
―单位矩阵的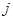 行的
行的 倍加到
倍加到 行或者单位矩阵的
行或者单位矩阵的 列的
列的 倍加到
倍加到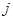 列所得到的矩阵。
列所得到的矩阵。
性质: 1) ; 2)
; 2)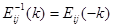 ;
;
3) 为将
为将 的
的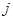 行的
行的 倍加到
倍加到 行所得到的矩阵,
行所得到的矩阵, 为将
为将 的
的 列的
列的 倍加到
倍加到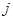 列所得到的矩阵。
列所得到的矩阵。
第四步 三个问题
【问题1】设 为
为 阶可逆矩阵,
阶可逆矩阵, 能够经过有限次初等行变换化为单位矩阵?
能够经过有限次初等行变换化为单位矩阵?
【问题2】 设 为
为 阶不可逆矩阵,
阶不可逆矩阵, 能够经过有限次初等行变换化为
能够经过有限次初等行变换化为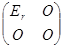 ?
?
【问题3】 设 为
为 阶不可逆矩阵,
阶不可逆矩阵, 能够经过有限次初等变换化为
能够经过有限次初等变换化为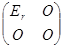 ?
?
第五步 初等变换法求逆阵及两个相关的定理
定理(初等变换法求逆阵)设 为
为 阶可逆矩阵,则
阶可逆矩阵,则 可以经过有限次初等行变换化为初等矩阵。
可以经过有限次初等行变换化为初等矩阵。
(二)矩阵的秩(记住:在方程组中矩阵的秩本质上就是约束条件)
1、定义―设 为
为 矩阵,若
矩阵,若 存在一个
存在一个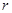 阶非零子式,但所有的
阶非零子式,但所有的 阶子式(如果有)都是零,则
阶子式(如果有)都是零,则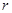 称为
称为 的秩,记为
的秩,记为 。
。
【注解】
(1)任何矩阵的秩都既不超过其行数也不超过其列数。设 为
为 矩阵,则
矩阵,则
 。
。
(2)设 为
为 阶矩阵,若
阶矩阵,若 ,则
,则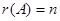 ,称
,称 为满秩矩阵。矩阵可逆、满秩及非奇异等价。
为满秩矩阵。矩阵可逆、满秩及非奇异等价。
2、矩阵秩的求法
将矩阵进行初等行变换阶梯化所得的非零行数即为矩阵的秩。
【注解】
(1)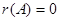 的充分必要条件是
的充分必要条件是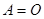 。
。
(2)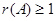 的充分必要条件是
的充分必要条件是 。
。
(3)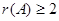 的充分必要条件是
的充分必要条件是 至少有两行不成比例。
至少有两行不成比例。
(4)设 ,则
,则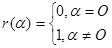 。
。
3、矩阵秩的性质
(1) 。
。
(2)设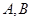 为同型矩阵,则
为同型矩阵,则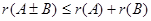 。
。
(3)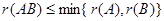 ,等价于
,等价于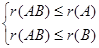 。
。
(4)设 为
为 矩阵,
矩阵,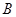 为
为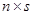 矩阵,且
矩阵,且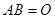 ,则
,则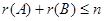 。
。
(5)设 为
为 矩阵,
矩阵,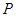 为
为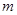 阶可逆阵,
阶可逆阵,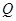 为
为 阶可逆阵,则有
阶可逆阵,则有
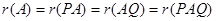 。
。
【矩阵秩例题】
【例题1】设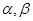 皆为三维列向量,
皆为三维列向量, ,证明:
,证明: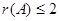 。
。
【例题2】设 为
为 阶可逆阵,证明
阶可逆阵,证明 的逆阵是唯一的。
的逆阵是唯一的。
【例题3】设 为
为 矩阵,
矩阵,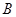 为
为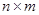 矩阵,其中
矩阵,其中 ,且
,且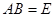 ,证明:
,证明: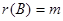 。
。
【例题4】设 为
为 阶矩阵,且
阶矩阵,且 ,证明:
,证明: 。
。
第二篇:考研数学线性代数必备结论
1、行列式
1.  行列式共有
行列式共有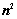 个元素,展开后有
个元素,展开后有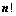 项,可分解为
项,可分解为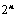 行列式;
行列式;
2. 代数余子式的性质:
①、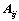 和
和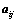 的大小无关;
的大小无关;
②、某行(列)的元素乘以其它行(列)元素的代数余子式为0;
③、某行(列)的元素乘以该行(列)元素的代数余子式为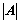 ;
;
3. 代数余子式和余子式的关系:
4. 设 行列式
行列式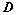 :
:
将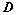 上、下翻转或左右翻转,所得行列式为
上、下翻转或左右翻转,所得行列式为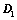 ,则
,则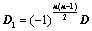 ;
;
将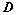 顺时针或逆时针旋转
顺时针或逆时针旋转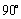 ,所得行列式为
,所得行列式为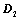 ,则
,则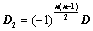 ;
;
将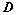 主对角线翻转后(转置),所得行列式为
主对角线翻转后(转置),所得行列式为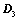 ,则
,则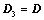 ;
;
将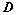 主副角线翻转后,所得行列式为
主副角线翻转后,所得行列式为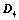 ,则
,则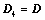 ;
;
5. 行列式的重要公式:
①、主对角行列式:主对角元素的乘积;
②、副对角行列式:副对角元素的乘积 ;
;
③、上、下三角行列式(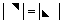 ):主对角元素的乘积;
):主对角元素的乘积;
④、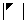 和
和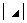 :副对角元素的乘积
:副对角元素的乘积 ;
;
⑤、拉普拉斯展开式: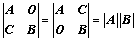 、
、
⑥、范德蒙行列式:大指标减小指标的连乘积;
⑦、特征值;
6. 对于 阶行列式
阶行列式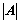 ,恒有:
,恒有: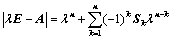 ,其中
,其中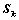 为
为 阶主子式;
阶主子式;
7. 证明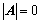 的方法:
的方法:
①、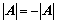 ;
;
②、反证法;
③、构造齐次方程组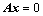 ,证明其有非零解;
,证明其有非零解;
④、利用秩,证明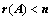 ;
;
⑤、证明0是其特征值;
2、矩阵
1.  是
是 阶可逆矩阵:
阶可逆矩阵:

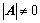 (是非奇异矩阵);
(是非奇异矩阵);

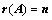 (是满秩矩阵)
(是满秩矩阵)

 的行(列)向量组线性无关;
的行(列)向量组线性无关;
 齐次方程组
齐次方程组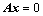 有非零解;
有非零解;

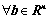 ,
, 总有唯一解;
总有唯一解;

 与
与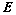 等价;
等价;

 可表示成若干个初等矩阵的乘积;
可表示成若干个初等矩阵的乘积;

 的特征值全不为0;
的特征值全不为0;

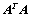 是正定矩阵;
是正定矩阵;

 的行(列)向量组是
的行(列)向量组是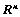 的一组基;
的一组基;

 是
是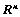 中某两组基的过渡矩阵;
中某两组基的过渡矩阵;
2. 对于 阶矩阵
阶矩阵 :
: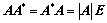 无条件恒成立;
无条件恒成立;
3. 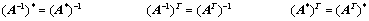

4. 矩阵是表格,推导符号为波浪号或箭头;行列式是数值,可求代数和;
5. 关于分块矩阵的重要结论,其中均 、
、 可逆:
可逆:
若 ,则:
,则:
Ⅰ、 ;
;
Ⅱ、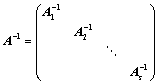 ;
;
②、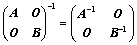 ;(主对角分块)
;(主对角分块)
③、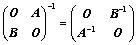 ;(副对角分块)
;(副对角分块)
④、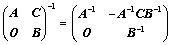 ;(拉普拉斯)
;(拉普拉斯)
⑤、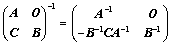 ;(拉普拉斯)
;(拉普拉斯)
3、矩阵的初等变换与线性方程组
1. 一个 矩阵
矩阵 ,总可经过初等变换化为标准形,其标准形是唯一确定的:
,总可经过初等变换化为标准形,其标准形是唯一确定的: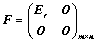 ;
;
等价类:所有与 等价的矩阵组成的一个集合,称为一个等价类;标准形为其形状最简单的矩阵;
等价的矩阵组成的一个集合,称为一个等价类;标准形为其形状最简单的矩阵;
对于同型矩阵 、
、 ,若
,若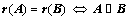 ;
;
2. 行最简形矩阵:
①、只能通过初等行变换获得;
②、每行首个非0元素必须为1;
③、每行首个非0元素所在列的其他元素必须为0;
3. 初等行变换的应用:(初等列变换类似,或转置后采用初等行变换)
①、 若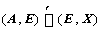 ,则
,则 可逆,且
可逆,且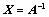 ;
;
②、对矩阵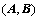 做初等行变化,当
做初等行变化,当 变为
变为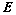 时,
时, 就变成
就变成 ,即:
,即: ;
;
③、求解线形方程组:对于 个未知数
个未知数 个方程
个方程 ,如果
,如果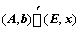 ,则
,则 可逆,且
可逆,且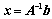 ;
;
4. 初等矩阵和对角矩阵的概念:
①、初等矩阵是行变换还是列变换,由其位置决定:左乘为初等行矩阵、右乘为初等列矩阵;
②、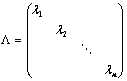 ,左乘矩阵
,左乘矩阵 ,
,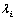 乘
乘 的各行元素;右乘,
的各行元素;右乘,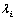 乘
乘 的各列元素;
的各列元素;
③、对调两行或两列,符号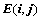 ,且
,且 ,例如:
,例如: ;
;
④、倍乘某行或某列,符号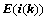 ,且
,且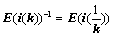 ,例如:
,例如: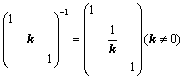 ;
;
⑤、倍加某行或某列,符号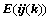 ,且
,且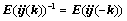 ,如:
,如: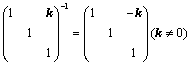 ;
;
5. 矩阵秩的基本性质:
①、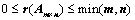 ;
;
②、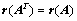 ;
;
③、若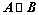 ,则
,则 ;
;
④、若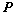 、
、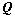 可逆,则
可逆,则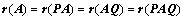 ;(可逆矩阵不影响矩阵的秩)
;(可逆矩阵不影响矩阵的秩)
⑤、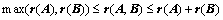 ;(※)
;(※)
⑥、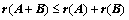 ;(※)
;(※)
⑦、 ;(※)
;(※)
⑧、如果 是
是 矩阵,
矩阵, 是
是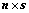 矩阵,且
矩阵,且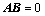 ,则:(※)
,则:(※)
Ⅰ、 的列向量全部是齐次方程组
的列向量全部是齐次方程组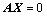 解(转置运算后的结论);
解(转置运算后的结论);
Ⅱ、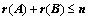
⑨、若 、
、 均为
均为 阶方阵,则
阶方阵,则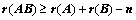 ;
;
6. 三种特殊矩阵的方幂:
①、秩为1的矩阵:一定可以分解为列矩阵(向量)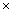 行矩阵(向量)的形式,再采用结合律;
行矩阵(向量)的形式,再采用结合律;
②、型如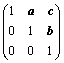 的矩阵:利用二项展开式;
的矩阵:利用二项展开式;
二项展开式: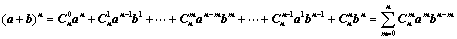 ;
;
注:Ⅰ、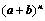 展开后有
展开后有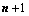 项;
项;
Ⅱ、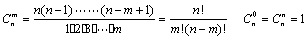
Ⅲ、组合的性质: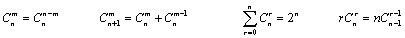 ;
;
③、利用特征值和相似对角化:
7. 伴随矩阵:
①、伴随矩阵的秩: ;
;
②、伴随矩阵的特征值: ;
;
③、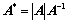 、
、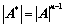
8. 关于 矩阵秩的描述:
矩阵秩的描述:
①、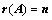 ,
, 中有
中有 阶子式不为0,
阶子式不为0,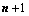 阶子式全部为0;(两句话)
阶子式全部为0;(两句话)
②、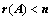 ,
, 中有
中有 阶子式全部为0;
阶子式全部为0;
③、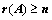 ,
, 中有
中有 阶子式不为0;
阶子式不为0;
9. 线性方程组: ,其中
,其中 为
为 矩阵,则:
矩阵,则:
①、 与方程的个数相同,即方程组
与方程的个数相同,即方程组 有
有 个方程;
个方程;
②、 与方程组得未知数个数相同,方程组
与方程组得未知数个数相同,方程组 为
为 元方程;
元方程;
10. 线性方程组 的求解:
的求解:
①、对增广矩阵 进行初等行变换(只能使用初等行变换);
进行初等行变换(只能使用初等行变换);
②、齐次解为对应齐次方程组的解;
③、特解:自由变量赋初值后求得;
11. 由 个未知数
个未知数 个方程的方程组构成
个方程的方程组构成 元线性方程:
元线性方程:
①、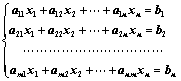 ;
;
②、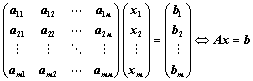 (向量方程,
(向量方程, 为
为 矩阵,
矩阵, 个方程,
个方程, 个未知数)
个未知数)
③、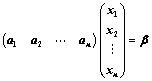 (全部按列分块,其中
(全部按列分块,其中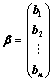 );
);
④、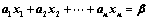 (线性表出)
(线性表出)
⑤、有解的充要条件: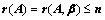 (
( 为未知数的个数或维数)
为未知数的个数或维数)
4、向量组的线性相关性
1.  个
个 维列向量所组成的向量组
维列向量所组成的向量组 :
: 构成
构成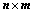 矩阵
矩阵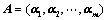 ;
;
 个
个 维行向量所组成的向量组
维行向量所组成的向量组 :
: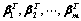 构成
构成 矩阵
矩阵 ;
;
含有有限个向量的有序向量组与矩阵一一对应;
2. ①、向量组的线性相关、无关 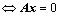 有、无非零解;(齐次线性方程组)
有、无非零解;(齐次线性方程组)
②、向量的线性表出  是否有解;(线性方程组)
是否有解;(线性方程组)
③、向量组的相互线性表示 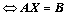 是否有解;(矩阵方程)
是否有解;(矩阵方程)
3. 矩阵 与
与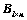 行向量组等价的充分必要条件是:齐次方程组
行向量组等价的充分必要条件是:齐次方程组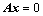 和
和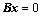 同解;(
同解;( 例14)
例14)
4. 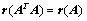 ;(
;( 例15)
例15)
5.  维向量线性相关的几何意义:
维向量线性相关的几何意义:
①、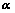 线性相关
线性相关 
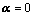 ;
;
②、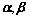 线性相关
线性相关 
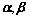 坐标成比例或共线(平行);
坐标成比例或共线(平行);
③、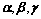 线性相关
线性相关 
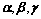 共面;
共面;
6. 线性相关与无关的两套定理:
若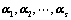 线性相关,则
线性相关,则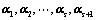 必线性相关;
必线性相关;
若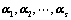 线性无关,则
线性无关,则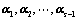 必线性无关;(向量的个数加加减减,二者为对偶)
必线性无关;(向量的个数加加减减,二者为对偶)
若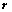 维向量组
维向量组 的每个向量上添上
的每个向量上添上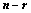 个分量,构成
个分量,构成 维向量组
维向量组 :
:
若 线性无关,则
线性无关,则 也线性无关;反之若
也线性无关;反之若 线性相关,则
线性相关,则 也线性相关;(向量组的维数加加减减)
也线性相关;(向量组的维数加加减减)
简言之:无关组延长后仍无关,反之,不确定;
7. 向量组 (个数为
(个数为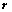 )能由向量组
)能由向量组 (个数为
(个数为 )线性表示,且
)线性表示,且 线性无关,则
线性无关,则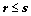 (二版
(二版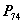 定理7);
定理7);
向量组 能由向量组
能由向量组 线性表示,则
线性表示,则 ;(
;(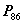 定理3)
定理3)
向量组 能由向量组
能由向量组 线性表示
线性表示
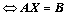 有解;
有解;
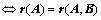 (
( 定理2)
定理2)
向量组 能由向量组
能由向量组 等价
等价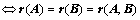 (
( 定理2推论)
定理2推论)
8. 方阵 可逆
可逆 存在有限个初等矩阵
存在有限个初等矩阵 ,使
,使 ;
;
①、矩阵行等价: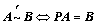 (左乘,
(左乘,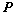 可逆)
可逆)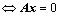 与
与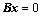 同解
同解
②、矩阵列等价: (右乘,
(右乘,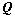 可逆);
可逆);
③、矩阵等价: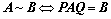 (
(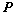 、
、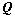 可逆);
可逆);
9. 对于矩阵 与
与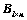 :
:
①、若 与
与 行等价,则
行等价,则 与
与 的行秩相等;
的行秩相等;
②、若 与
与 行等价,则
行等价,则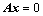 与
与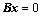 同解,且
同解,且 与
与 的任何对应的列向量组具有相同的线性相关性;
的任何对应的列向量组具有相同的线性相关性;
③、矩阵的初等变换不改变矩阵的秩;
④、矩阵 的行秩等于列秩;
的行秩等于列秩;
10. 若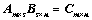 ,则:
,则:
①、 的列向量组能由
的列向量组能由 的列向量组线性表示,
的列向量组线性表示, 为系数矩阵;
为系数矩阵;
②、 的行向量组能由
的行向量组能由 的行向量组线性表示,
的行向量组线性表示,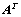 为系数矩阵;(转置)
为系数矩阵;(转置)
11. 齐次方程组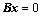 的解一定是
的解一定是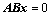 的解,考试中可以直接作为定理使用,而无需证明;
的解,考试中可以直接作为定理使用,而无需证明;
①、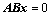 只有零解
只有零解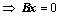 只有零解;
只有零解;
②、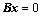 有非零解
有非零解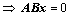 一定存在非零解;
一定存在非零解;
12. 设向量组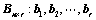 可由向量组
可由向量组 线性表示为:(
线性表示为:( 题19结论)
题19结论)
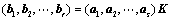 (
(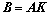 )
)
其中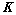 为
为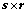 ,且
,且 线性无关,则
线性无关,则 组线性无关
组线性无关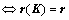 ;(
;( 与
与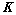 的列向量组具有相同线性相关性)
的列向量组具有相同线性相关性)
(必要性: ;充分性:反证法)
;充分性:反证法)
注:当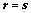 时,
时,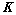 为方阵,可当作定理使用;
为方阵,可当作定理使用;
13. ①、对矩阵 ,存在
,存在 ,
,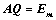
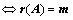 、
、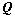 的列向量线性无关;(
的列向量线性无关;(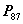 )
)
②、对矩阵 ,存在
,存在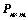 ,
,
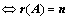 、
、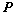 的行向量线性无关;
的行向量线性无关;
14. 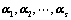 线性相关
线性相关
 存在一组不全为0的数
存在一组不全为0的数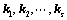 ,使得
,使得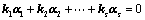 成立;(定义)
成立;(定义)

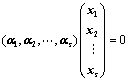 有非零解,即
有非零解,即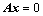 有非零解;
有非零解;

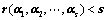 ,系数矩阵的秩小于未知数的个数;
,系数矩阵的秩小于未知数的个数;
15. 设 的矩阵
的矩阵 的秩为
的秩为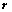 ,则
,则 元齐次线性方程组
元齐次线性方程组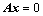 的解集
的解集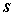 的秩为:
的秩为: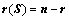 ;
;
16. 若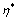 为
为 的一个解,
的一个解, 为
为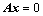 的一个基础解系,则
的一个基础解系,则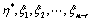 线性无关;(
线性无关;( 题33结论)
题33结论)
5、相似矩阵和二次型
1. 正交矩阵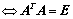 或
或 (定义),性质:
(定义),性质:
①、 的列向量都是单位向量,且两两正交,即
的列向量都是单位向量,且两两正交,即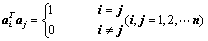 ;
;
②、若 为正交矩阵,则
为正交矩阵,则 也为正交阵,且
也为正交阵,且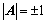 ;
;
③、若 、
、 正交阵,则
正交阵,则 也是正交阵;
也是正交阵;
注意:求解正交阵,千万不要忘记施密特正交化和单位化;
2. 施密特正交化: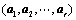
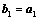 ;
;


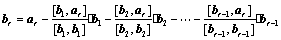 ;
;
3. 对于普通方阵,不同特征值对应的特征向量线性无关;
对于实对称阵,不同特征值对应的特征向量正交;
4. ①、 与
与 等价
等价 
 经过初等变换得到
经过初等变换得到 ;
;
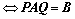 ,
,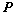 、
、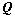 可逆;
可逆;
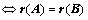 ,
, 、
、 同型;
同型;
②、 与
与 合同
合同 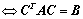 ,其中可逆;
,其中可逆;
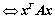 与
与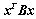 有相同的正、负惯性指数;
有相同的正、负惯性指数;
③、 与
与 相似
相似 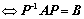 ;
;
5. 相似一定合同、合同未必相似;
若 为正交矩阵,则
为正交矩阵,则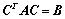
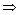
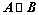 ,(合同、相似的约束条件不同,相似的更严格);
,(合同、相似的约束条件不同,相似的更严格);
6.  为对称阵,则
为对称阵,则 为二次型矩阵;
为二次型矩阵;
7.  元二次型
元二次型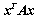 为正定:
为正定:
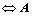 的正惯性指数为
的正惯性指数为 ;
;
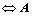 与
与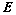 合同,即存在可逆矩阵
合同,即存在可逆矩阵 ,使
,使 ;
;
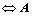 的所有特征值均为正数;
的所有特征值均为正数;
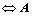 的各阶顺序主子式均大于0;
的各阶顺序主子式均大于0;
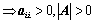 ;(必要条件)
;(必要条件)
