20xx最新高考数学专题总结立体几何重点题型空间距离空间角(生)
立体几何重点题型
【考点透视】
(A)版.掌握两条直线所成的角和距离的概念,对于异面直线的距离,只要求会计算已给出公垂线时的距离.掌握斜线在平面上的射影、直线和平面所成的角、直线和平面的距离的概念.掌握二面角、二面角的平面角、两个平行平面间的距离的概念.
(B)版.
①理解空间向量的概念,掌握空间向量的加法、减法和数乘.
②了解空间向量的基本定理,理解空间向量坐标的概念,掌握空间向量的坐标运算.
③掌握空间向量的数量积的定义及其性质,掌握用直角坐标计算空间向量数量积公式.
④理解直线的方向向量、平面的法向量,向量在平面内的射影等概念.
⑤了解多面体、凸多面体、正多面体、棱柱、棱锥、球的概念.
⑥掌握棱柱、棱锥、球的性质,掌握球的表面积、体积公式.
⑦会画直棱柱、正棱锥的直观图.
空间距离和角是高考考查的重点:特别是以两点间距离,点到平面的距离,两异面直线的距离,直线与平面的距离以及两异面直线所成的角,直线与平面所成的角,二面角等作为命题的重点内容,高考试题中常将上述内容综合在一起放在解答题中进行考查,分为多个小问题,也可能作为客观题进行单独考查.考查空间距离和角的试题一般作为整套试卷的中档题,但也可能在最后一问中设置有难度的问题.
不论是求空间距离还是空间角,都要按照“一作,二证,三算”的步骤来完成,即寓证明于运算之中,正是本专题的一大特色.
求解空间距离和角的方法有两种:一是利用传统的几何方法,二是利用空间向量。
【例题解析】
考点1 点到平面的距离
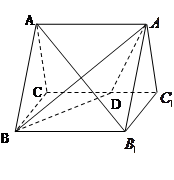 求点到平面的距离就是求点到平面的垂线段的长度,其关键在于确定点在平面内的垂足,当然别忘了转化法与等体积法的应用.
求点到平面的距离就是求点到平面的垂线段的长度,其关键在于确定点在平面内的垂足,当然别忘了转化法与等体积法的应用.
典型例题
例1如图,正三棱柱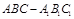 的所有棱长都为
的所有棱长都为 ,
,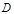 为
为 中点.
中点.
(Ⅰ)求证: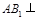 平面
平面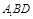 ;
;
(Ⅱ)求二面角 的大小;
的大小;
(Ⅲ)求点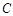 到平面
到平面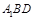 的距离.
的距离.
例2.如图,已知两个正四棱锥P-ABCD与Q-ABCD的高分别为1和2,AB=4.
(Ⅰ)证明PQ⊥平面ABCD;
(Ⅱ)求异面直线AQ与PB所成的角;
(Ⅲ)求点P到平面QAD的距离.
考点2 异面直线的距离
 此类题目主要考查异面直线的距离的概念及其求法,考纲只要求掌握已给出公垂线段的异面直线的距离.
此类题目主要考查异面直线的距离的概念及其求法,考纲只要求掌握已给出公垂线段的异面直线的距离.
典型例题
例3 已知三棱锥 ,底面是边长为
,底面是边长为 的正三角形,棱
的正三角形,棱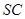 的长为2,且垂直于底面.
的长为2,且垂直于底面.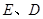 分别为
分别为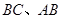 的中点,求CD与SE间的距离.
的中点,求CD与SE间的距离.
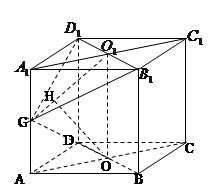 考点3 直线到平面的距离
考点3 直线到平面的距离
此类题目再加上平行平面间的距离,主要考查点面、线面、面面距离间的转化.
典型例题
例4.如图,在棱长为2的正方体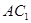 中,G是
中,G是 的中点,
的中点,
求BD到平面 的距离.
的距离.
考点4 异面直线所成的角
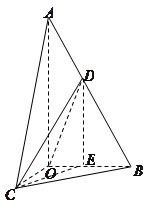 此类题目一般是按定义作出异面直线所成的角,然后通过解三角形来求角.异面直线所成的角是高考考查的重点.
此类题目一般是按定义作出异面直线所成的角,然后通过解三角形来求角.异面直线所成的角是高考考查的重点.
典型例题
例5如图,在 中,
中,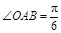 ,斜边
,斜边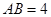 .
.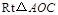 可以通过
可以通过 以直线
以直线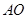 为轴旋转得到,且二面角
为轴旋转得到,且二面角 的直二面角.
的直二面角. 是
是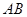 的中点.
的中点.
 (I)求证:平面
(I)求证:平面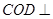 平面
平面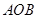 ;
;
(II)求异面直线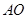 与
与 所成角的大小.
所成角的大小.
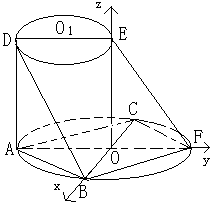
例6.如图所示,AF、DE分别是⊙O、⊙O1的直径.AD与两圆所在的平面均垂直,AD=8,BC是⊙O的直径,AB=AC=6,OE//AD.
(Ⅰ)求二面角B―AD―F的大小;
(Ⅱ)求直线BD与EF所成的角.
考点5 直线和平面所成的角
此类题主要考查直线与平面所成的角的作法、证明以及计算.
线面角在空间角中占有重要地位,是高考的常考内容.
典型例题
 例7. 四棱锥
例7. 四棱锥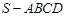 中,底面
中,底面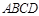 为平行四边形,侧面
为平行四边形,侧面 底面
底面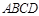 .已知
.已知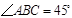 ,
,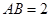 ,
, ,
,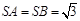 .
.
(Ⅰ)证明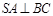 ;
;
(Ⅱ)求直线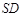 与平面
与平面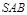 所成角的大小.
所成角的大小.
考点6 二面角
此类题主要是如何确定二面角的平面角,并将二面角的平面角转化为线线角放到一个合适的三角形中进行求解.二面角是高考的热点,应重视.
典型例题
例8.如图,已知直二面角 ,
,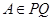 ,
,
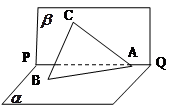 ,
,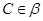 ,
,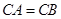 ,
,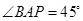 ,直线
,直线 和平面
和平面 所成的角为
所成的角为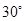 .
.
(I)证明 ;
;
(II)求二面角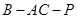 的大小.
的大小.
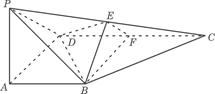 例9.如图,在四棱锥P-ABCD中,PA
例9.如图,在四棱锥P-ABCD中,PA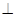 底面ABCD,
底面ABCD, DAB为直角,AB‖CD,AD=CD=2AB, E、F分别为PC、CD的中点.
DAB为直角,AB‖CD,AD=CD=2AB, E、F分别为PC、CD的中点.
(Ⅰ)试证:CD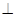 平面BEF;
平面BEF;
(Ⅱ)设PA=k·AB,且二面角E-BD-C的平面角大于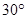 ,求k的取值范围.
,求k的取值范围.
 考点7 利用空间向量求空间距离和角
考点7 利用空间向量求空间距离和角
众所周知,利用空间向量求空间距离和角的套路与格式固定.当掌握了用向量的方法解决立体几何问题这套强有力的工具时,不仅会降低题目的难度,而且使得作题具有很强的操作性.
典型例题
例10. 如图,已知 是棱长为
是棱长为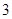 的正方体,
的正方体,
点 在
在 上,点
上,点 在
在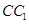 上,且
上,且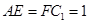 .
.
(1)求证: 四点共面;
四点共面;
(2)若点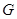 在
在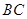 上,
上, ,点
,点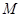 在
在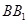 上,
上,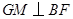 ,垂足为
,垂足为 ,求证:
,求证:
 平面
平面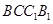 ;
;
(3)用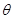 表示截面
表示截面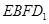 和侧面
和侧面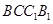 所成的锐二面角的大小,求
所成的锐二面角的大小,求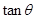 .
.
例11.如图,l1、l2是互相垂直的两条异面直线,MN是它们的公垂线段,点A、B在l1上,C在l2上,AM=MB=MN
(I)证明AC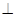 NB;
NB;
(II)若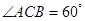 ,求NB与平面ABC所成角的余弦值.
,求NB与平面ABC所成角的余弦值.
考点8 简单多面体的有关概念及应用
主要考查多面体的概念、性质,主要以填空、选择题为主,通常结合多面体的定义、性质进行判断.
典型例题
例12 . 如图(1),将边长为1的正六边形铁皮的六个角各切去一个全等的四边形,再沿虚线折起,做成一个无盖的正六棱柱容器,当这个正六棱柱容器的底面边长为 时容积最大.
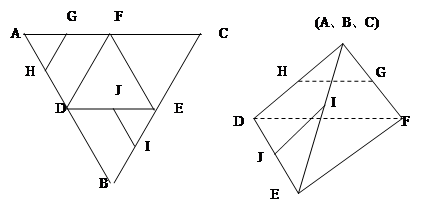 例13 .如图左,在正三角形ABC中,D、E、F分别为各边的中点,G、H、I、J分别为AF、AD、BE、DE的中点,将△ABC沿DE、EF、DF折成三棱锥后,GH与IJ所成角的度数为( )
例13 .如图左,在正三角形ABC中,D、E、F分别为各边的中点,G、H、I、J分别为AF、AD、BE、DE的中点,将△ABC沿DE、EF、DF折成三棱锥后,GH与IJ所成角的度数为( )
 A、90° B、60° C、45° D、0°
A、90° B、60° C、45° D、0°
例14.长方体ABCD-A1B1C1D1中,
设对角线D1B与自D1出发的三条棱分别成α、β、
 角
角
求证:cos2α+cos2β+cos2 =1
=1
设D1B与自D1出发的三个面成α、β、 角,求证:
角,求证:
cos2α+cos2β+cos2 =2
=2
考点9.简单多面体的侧面积及体积和球的计算
棱柱侧面积转化成求矩形或平行四边形面积,棱柱侧面积转化成求三角形的面积.
直棱柱体积V等于底面积与高的乘积.
棱锥体积V等于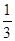 Sh其中S是底面积,h是棱锥的高.
Sh其中S是底面积,h是棱锥的高.
典型例题
例15. 如图,在三棱柱ABC-A1B1C1中,AB=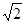 a,BC=CA=AA1=a,
a,BC=CA=AA1=a,
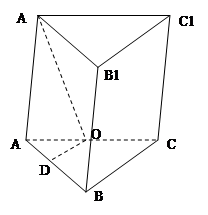 A1在底面△ABC上的射影O在AC上
A1在底面△ABC上的射影O在AC上
求AB与侧面AC1所成角;
若O恰好是AC的中点,求此三棱柱的侧面积.
例16. 等边三角形ABC的边长为4,M、N分别为AB、AC的中点,沿MN将△AMN折起,使得面AMN与面MNCB所成的二面角为30°,则四棱锥A―MNCB的体积为 ( )
A、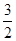 B、
B、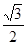 C、
C、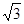 D、3
D、3
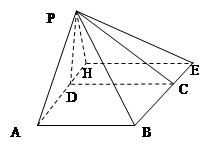 例17.如图,四棱锥P―ABCD中,底面是一个矩形,AB=3,AD=1,又PA⊥AB,PA=4,∠PAD=60°
例17.如图,四棱锥P―ABCD中,底面是一个矩形,AB=3,AD=1,又PA⊥AB,PA=4,∠PAD=60°
求四棱锥的体积;
求二面角P-BC-D的大小.
 例18 .已知圆O1是半径为R的球O的一个小圆,且圆O1的面积与球O的表面积的比值为
例18 .已知圆O1是半径为R的球O的一个小圆,且圆O1的面积与球O的表面积的比值为 ,则线段OO1与R的比值为 .
,则线段OO1与R的比值为 .
第二篇:20xx届高考数学知识点总结 立体几何
高中数学第九章-立体几何
考试内容
平面及其基本性质.平面图形直观图的画法.
平行直线.对应边分别平行的角.异面直线所成的角.异面直线的公垂线.异面直线的距离.
直线和平面平行的判定与性质.直线和平面垂直的判定与性质.点到平面的距离.斜线在平面上的射影.直线和平面所成的角.三垂线定理及其逆定理.
平行平面的判定与性质.平行平面间的距离.二面角及其平面角.两个平面垂直的判定与性质.
多面体.正多面体.棱柱.棱锥.球.
考试要求
(1)掌握平面的基本性质,会用斜二测的画法画水平放置的平面图形的直观图;能够画出空间两条直线、直线和平面的各种位置关系的图形,能够根据图形想像它们的位置关系.
(2)掌握两条直线平行与垂直的判定定理和性质定理,掌握两条直线所成的角和距离的概念,对于异面直线的距离,只要求会计算已给出公垂线时的距离.
(3)掌握直线和平面平行的判定定理和性质定理;掌握直线和平面垂直的判定定理和性质定理;掌握斜线在平面上的射影、直线和平面所成的角、直线和平面的距离的概念掌握三垂线定理及其逆定理.
(4)掌握两个平面平行的判定定理和性质定理,掌握二面角、二面角的平面角、两个平行平面间的距离的概念,掌握两个平面垂直的判定定理和性质定理.
(5)会用反证法证明简单的问题.
(6)了解多面体、凸多面体的概念,了解正多面体的概念.
(7)了解棱柱的概念,掌握棱柱的性质,会画直棱柱的直观图.
(8)了解棱锥的概念,掌握正棱锥的性质,会画正棱锥的直观图.
(9)了解球的概念,掌握球的性质,掌握球的表面积、体积公式.
9(B).直线、平面、简单几何体
考试内容:
平面及其基本性质.平面图形直观图的画法.
平行直线.
直线和平面平行的判定与性质.直线和平面垂直的判定.三垂线定理及其逆定理.
两个平面的位置关系.
空间向量及其加法、减法与数乘.空间向量的坐标表示.空间向量的数量积.
直线的方向向量.异面直线所成的角.异面直线的公垂线.异面直线的距离.
直线和平面垂直的性质.平面的法向量.点到平面的距离.直线和平面所成的角.向量在平面内的射影.
平行平面的判定和性质.平行平面间的距离.二面角及其平面角.两个平面垂直的判定和性质.
多面体.正多面体.棱柱.棱锥.球.
考试要求:
(1)掌握平面的基本性质。会用斜二测的画法画水平放置的平面图形的直观图:能够画出空间两条直线、直线和平面的各种位置关系的图形.能够根据图形想像它们的位置关系.
(2)掌握直线和平面平行的判定定理和性质定理;理解直线和平面垂直的概念.掌握直线和平面垂直的判定定理;掌握三垂线定理及其逆定理.
(3)理解空间向量的概念,掌握空间向量的加法、减法和数乘.
(4)了解空间向量的基本定理;理解空间向量坐标的概念.掌握空间向量的坐标运算.
(5)掌握空间向量的数量积的定义及其性质:掌握用直角坐标计算空间向量数量积的公式;掌握空间两点间距离公式.
(6)理解直线的方向向量、平面的法向量、向量在平面内的射影等概念.
(7)掌握直线和直线、直线和平面、平面和平面所成的角、距离的概念.对于异面直线的距离,只要求会计算已给出公垂线或在坐标表示下的距离掌握直线和平面垂直的性质定理掌握两个平面平行、垂直的判定定理和性质定理.
(8)了解多面体、凸多面体的概念。了解正多面体的概念.
(9)了解棱柱的概念,掌握棱柱的性质,会画直棱柱的直观图.
(10)了解棱锥的概念,掌握正棱锥的性质。会画正棱锥的直观图.
(11)了解球的概念.掌握球的性质.掌握球的表面积、体积公式.
(考生可在9(A)和9(B)中任选其一)
立体几何知识要点
一、知识提纲
(一)空间的直线与平面
⒈平面的基本性质 ⑴三个公理及公理三的三个推论和它们的用途. ⑵斜二测画法.
⒉空间两条直线的位置关系:相交直线、平行直线、异面直线.
⑴公理四(平行线的传递性).等角定理.
⑵异面直线的判定:判定定理、反证法.
⑶异面直线所成的角:定义(求法)、范围.
⒊直线和平面平行 直线和平面的位置关系、直线和平面平行的判定与性质.
⒋直线和平面垂直
⑴直线和平面垂直:定义、判定定理.
⑵三垂线定理及逆定理.
5.平面和平面平行
两个平面的位置关系、两个平面平行的判定与性质.
6.平面和平面垂直
互相垂直的平面及其判定定理、性质定理.
(二)直线与平面的平行和垂直的证明思路(见附图)
(三)夹角与距离
7.直线和平面所成的角与二面角
⑴平面的斜线和平面所成的角:三面角余弦公式、最小角定理、斜线和平
面所成的角、直线和平面所成的角.
⑵二面角:①定义、范围、二面角的平面角、直二面角.
②互相垂直的平面及其判定定理、性质定理.
8.距离
⑴点到平面的距离.
⑵直线到与它平行平面的距离.
⑶两个平行平面的距离:两个平行平面的公垂线、公垂线段.
⑷异面直线的距离:异面直线的公垂线及其性质、公垂线段.
(四)简单多面体与球
9.棱柱与棱锥
⑴多面体.
⑵棱柱与它的性质:棱柱、直棱柱、正棱柱、棱柱的性质.
⑶平行六面体与长方体:平行六面体、直平行六面体、长方体、正四棱柱、
正方体;平行六面体的性质、长方体的性质.
⑷棱锥与它的性质:棱锥、正棱锥、棱锥的性质、正棱锥的性质.
⑸直棱柱和正棱锥的直观图的画法.
10.多面体欧拉定理的发现
⑴简单多面体的欧拉公式.
⑵正多面体.
11.球
⑴球和它的性质:球体、球面、球的大圆、小圆、球面距离.
⑵球的体积公式和表面积公式.
二、常用结论、方法和公式
1.从一点O出发的三条射线OA、OB、OC,若∠AOB=∠AOC,则点A在平面∠BOC上的射影在∠BOC的平分线上;
2. 已知:直二面角M-AB-N中,AE 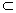 M,BF
M,BF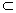 N,∠EAB=
N,∠EAB=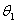 ,∠ABF=
,∠ABF=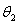 ,异面直线AE与BF所成的角为
,异面直线AE与BF所成的角为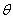 ,则
,则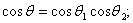
3.立平斜公式:如图,AB和平面所成的角是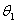 ,AC在平面内,BC和AB的射影BA1成
,AC在平面内,BC和AB的射影BA1成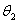 ,设∠ABC=
,设∠ABC=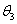 ,则cos
,则cos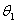 cos
cos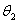 =cos
=cos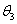 ;
;

4.异面直线所成角的求法:
(1)平移法:在异面直线中的一条直线中选择一特殊点,作另一条的平行线;
(2)补形法:把空间图形补成熟悉的或完整的几何体,如正方体、平行六面体、长方体等,其目的在于容易发现两条异面直线间的关系;
5.直线与平面所成的角
斜线和平面所成的是一个直角三角形的锐角,它的三条边分别是平面的垂线段、斜线段及斜线段在平面上的射影。通常通过斜线上某个特殊点作出平面的垂线段,垂足和斜足的连线,是产生线面角的关键;
6.二面角的求法
(1)定义法:直接在二面角的棱上取一点(特殊点),分别在两个半平面内作棱的垂线,得出平面角,用定义法时,要认真观察图形的特性;
(2)三垂线法:已知二面角其中一个面内一点到一个面的垂线,用三垂线定理或逆定理作出二面角的平面角;
(3)垂面法:已知二面角内一点到两个面的垂线时,过两垂线作平面与两个半平面的交线所成的角即为平面角,由此可知,二面角的平面角所在的平面与棱垂直;
(4)射影法:利用面积射影公式S射=S原cos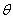 ,其中
,其中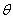 为平面角的大小,此法不必在图形中画出平面角;
为平面角的大小,此法不必在图形中画出平面角;
特别:对于一类没有给出棱的二面角,应先延伸两个半平面,使之相交出现棱,然后再选用上述方法(尤其要考虑射影法)。
7.空间距离的求法
(1)两异面直线间的距离,高考要求是给出公垂线,所以一般先利用垂直作出公垂线,然后再进行计算;
(2)求点到直线的距离,一般用三垂线定理作出垂线再求解;
(3)求点到平面的距离,一是用垂面法,借助面面垂直的性质来作,因此,确定已知面的垂面是关键;二是不作出公垂线,转化为求三棱锥的高,利用等体积法列方程求解;
8.正棱锥的各侧面与底面所成的角相等,记为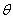 ,则S侧cos
,则S侧cos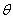 =S底;
=S底;
9.已知:长方体的体对角线与过同一顶点的三条棱所成的角分别为 因此有cos2
因此有cos2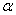 +cos2
+cos2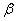 +cos2
+cos2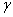 =1; 若长方体的体对角线与过同一顶点的三侧面所成的角分别为
=1; 若长方体的体对角线与过同一顶点的三侧面所成的角分别为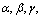 则有cos2
则有cos2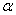 +cos2
+cos2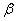 +cos2
+cos2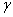 =2;
=2;
10.正方体和长方体的外接球的直径等与其体对角线长;
11.欧拉公式:如果简单多面体的顶点数为V,面数为F,棱数为E.那么V+F-E=2;并且棱数E=各顶点连着的棱数和的一半=各面边数和的一半;
12.柱体的体积公式:柱体(棱柱、圆柱)的体积公式是V柱体=Sh.其中S是柱体的底面积,h是柱体的高.
13.直棱柱的侧面积和全面积
S直棱柱侧= c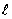 (c表示底面周长,
(c表示底面周长,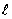 表示侧棱长) S棱柱全=S底+S侧
表示侧棱长) S棱柱全=S底+S侧
14.棱锥的体积:V棱锥=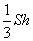 ,其中S是棱锥的底面积,h是棱锥的高。
,其中S是棱锥的底面积,h是棱锥的高。
15.球的体积公式V=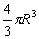 ,表面积公式
,表面积公式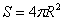 ;掌握球面上两点A、B间的距离求法:(1)计算线段AB的长,(2)计算球心角∠AOB的弧度数;(3)用弧长公式计算劣弧AB的长。
;掌握球面上两点A、B间的距离求法:(1)计算线段AB的长,(2)计算球心角∠AOB的弧度数;(3)用弧长公式计算劣弧AB的长。
