数列求和方法总结
数列求和的基本方法和技巧
数列是高中代数的重要内容,又是学习高等数学的基础。 在高考和各种数学竞赛中都占有重要的地位。 数列求和是数列的重要内容之一,除了等差数列和等比数列有求和公式外,大部分数列的求和都需要一定的技巧。 下面,就几个历届高考数学和数学竞赛试题来谈谈数列求和的基本方法和技巧。
一、公式法
利用下列常用求和公式求和是数列求和的最基本最重要的方法。
1、 差数列求和公式:Sn(a1?an)n?
2?na?n(n?1)
12
d ?na1(q?1)2、等比数列求和公式:S???an
n?1(1?q)a1?1?q
??anq1?q(q?1)
n
3、S??k?1n
(n?1) 4、S2
1nn?k?1
2?k?(n?1)(2n?1)
k?16n4、Sn?
?k
3
?[1
(n?1)]2k?1
2
例 :已知log?123x?
log,求x?x?x3?????xn
????的前n项和. 23
解:由log13x?
?log3?log??log1
3x32?x?2
2 由等比数列求和公式得 Sn?x?x2?x3?????xn
=x(1?xn)
1?x
1(1?1=n)
1?12=1-12
n
解析:如果计算过程中出现了这些关于n的多项式的求和形式,可以直接利用公式。
二、错位相减
这种方法是在推导等比数列的前n项和公式时所用的方法,这种方法主要用于求数列{an・项和,其中{ an }、{ bn }分别是等差数列和等比数列。
bn}的前n
例:求数列a,2a2,3a3,4a4,…,nan, …(a为常数)的前n项和。 解:若a=0, 则Sn=0
若a=1,
则Sn=1+2+3+…+n= 若a≠0且a≠1
则Sn=a+2a2+3a3+4a4+…+ nan ∴aSn= a2+2 a3+3 a4+…+nan+1 ∴(1-a) Sn=a+ a2+ a3+…+an- nan+1
n?1
a?a= ?nan?11?a
n(n?1)2
n?1n?1
a?ana ∴Sn= ?(a?1)2(1?a)1?a
当a=0时,此式也成立。 ∴Sn=
n(n?1)
(a?1)2
a?an?1nan?1
?(a?1)2
(1?a)1?a
解析:数列是由数列?n?与an对应项的积构成的,此类型的才适应错位相减,(课本中的的等比数列前n项和公式就是用这种方法推导出来的),但要注意应按以上三种情况进行讨论,最后再综合成两种情况。
三、倒序相加
这是推导等差数列的前n项和公式时所用的方法,就是将一个数列倒过来排列(反序),再把它与原数列相加,就可以得到n个(a1?an)。
[例5] 求证:Cn?3Cn?5Cn?????(2n?1)Cn?(n?1)2
证明: 设Sn?Cn?3Cn?5Cn?????(2n?1)Cn………………………….. ① 把①式右边倒转过来得
nn?110
(反序) Sn?(2n?1)Cn?(2n?1)Cn?????3Cn?Cn
1
2
n
1
2
n
n
???
又由Cn?Cn
mn?m
可得
1
n?1
n
…………..…….. ② ?Cn
Sn?(2n?1)Cn?(2n?1)Cn?????3Cn
01n?1n
①+②得 2Sn?(2n?2)(Cn?Cn?????Cn?Cn)?2(n?1)?2n (反序相加)
∴ Sn?(n?1)?2n
解析:此类型关键是抓住数列中与首末两端等距离的两项之和相等这一特点来进行倒序相加的。
四、分组求和
有一类数列,既不是等差数列,也不是等比数列,若将这类数列适当拆开,可分为几个等差、等比或常见的数列,然后分别求和,再将其合并即可。
例:Sn=-1+3-5+7-…+(-1)n(2n-1)
解法:按n为奇偶数进行分组,连续两项为一组。 当n为奇数时:
Sn=(-1+3)+(-5+7)+(-9+11)+…+(-2n+1) =2×
n?1
+(-2n+1) 2
=-n
当n为偶数时:
Sn=(-1+3)+(-5+7)+(-9+11)+…+[(-2n+3)+(2n+1)] =2× =n ∴Sn=
n 2
五、裂项法求和
这是分解与组合思想在数列求和中的具体应用。 裂项法的实质是将数列中的每项(通项)分解,然后
重新组合,使之能消去一些项,最终达到求和的目的通项分解(裂项)如: (1)an?f(n?1)?f(n) (2)
sin1
?tan(n?1)?tann
cosncos(n?1)
111(2n)2111
??(3)an? (4)an??1?(?)
n(n?1)nn?1(2n?1)(2n?1)22n?12n?1
(5)an?
1111
?[?]
n(n?1)(n?2)2n(n?1)(n?1)(n?2)
(6) an?
n?212(n?1)?n1111
?n??n??,则S?1? nn?1nn
n(n?1)2n(n?1)2n?2(n?1)2(n?1)21111
,,,…,,…的前n项和S 1?32?43?5n(n?2)
例:求数列
解:∵
1111
=(?)
n(n?2)2nn?2
Sn=
1?11111?(1?)?(?)?????(?)? 2?324nn?2??
1111(1???) 22n?1n?2311
? =?
42n?22n?4
=
解析:要先观察通项类型,在裂项求和,而且要注意剩下首尾两项,还是剩下象上例中的四项,后面还很可能和极限、求参数的最大小值联系。
六、合并求和
针对一些特殊的数列,将某些项合并在一起就具有某种特殊的性质,因此,在求数列的和时,可将这些项放在一起先求和,然后再求Sn.
例: 数列{an}:a1?1,a2?3,a3?2,an?2?an?1?an,求S20xx.
解:设S20xx=a1?a2?a3?????a20xx
由a1?1,a2?3,a3?2,an?2?an?1?an可得
a4??1,a5??3,a6??2,
a7?1,a8?3,a9?2,a10??1,a11??3,a12??2,
……
a6k?1?1,a6k?2?3,a6k?3?2,a6k?4??1,a6k?5??3,a6k?6??2
∵ a6k?1?a6k?2?a6k?3?a6k?4?a6k?5?a6k?6?0 (找特殊性质项) ∴ S20xx=a1?a2?a3?????a20xx (合并求和) =(a1?a2?a3????a6)?(a7?a8????a12)?????(a6k?1?a6k?2?????a6k?6)
?????(a1993?a1994?????a1998)?a1999?a20xx?a20xx?a20xx
=a1999?a20xx?a20xx?a20xx =a6k?1?a6k?2?a6k?3?a6k?4 =5
七、拆项求和
先研究通项,通项可以分解成几个等差或等比数列的和或差的形式,再代入公式求和。
例:求数5,55,555,…,的前n项和Sn
解: 因为5n
9
(10?1)
所以 Sn=5+55+555+… =
5
?(10?1)?(102?1)?????(10n9
?1)?
=5?10(10n?1)
?9?10?1?n?
??
=
5081?10n?59n?5081
解析:根据通项的特点,通项可以拆成两项或三项的常见数列,然后再分别求和。另外:S1n=12?214?3118?????n2
n 可以拆成:S…+n)+(1111
n=(1+2+3+2?4?8?????2
n)
第二篇:数列求和方法总结
课题: 数列求和的基本方法和技巧
兰州三十四中----王永生
教学目标:

教学重点与难点:

教学过程:
数列是高中代数的重要内容,又是学习高等数学的基础。 在高考和各种数学竞赛中都占有重要的地位。 数列求和是数列的重要内容之一,除了等差数列和等比数列有求和公式外,大部分数列的求和都需要一定的技巧。 下面,就几个历届高考数学和数学竞赛试题来谈谈数列求和的基本方法和技巧。
一、公式法
利用下列常用求和公式求和是数列求和的最基本最重要的方法。
1、 差数列求和公式: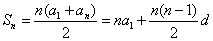
2、等比数列求和公式: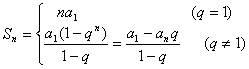
3、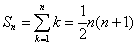 4、
4、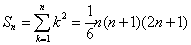 5、
5、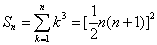
例 :已知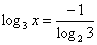 ,求
,求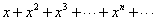 的前n项和.
的前n项和.
解:由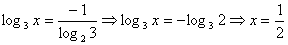
由等比数列求和公式得 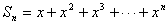 =
=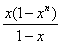 =
=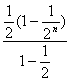 =1-
=1-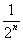
解析:如果计算过程中出现了这些关于n的多项式的求和形式,可以直接利用公式。
二、错位相减
这种方法是在推导等比数列的前n项和公式时所用的方法,这种方法主要用于求数列{an· bn}的前n项和,其中{ an }、{ bn }分别是等差数列和等比数列。
例:求数列a,2a2,3a3,4a4,…,nan, …(a为常数)的前n项和。
解:若a=0, 则Sn=0
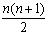 若a=1, 则Sn=1+2+3+…+n=
若a=1, 则Sn=1+2+3+…+n=
若a≠0且a≠1 则
∴aSn= a2+2 a3+3 a4+…+nan+1
∴(1-a) Sn=a+ a2+ a3+…+an- nan+1
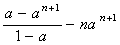 =
=
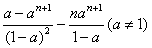 ∴Sn=
∴Sn=
当a=0时,此式也成立。

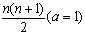
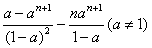 ∴Sn=
∴Sn=
解析:数列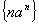 是由数列
是由数列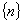 与
与 对应项的积构成的,此类型的才适应错位相减,(课本中的的等比数列前n项和公式就是用这种方法推导出来的),但要注意应按以上三种情况进行讨论,最后再综合成两种情况。
对应项的积构成的,此类型的才适应错位相减,(课本中的的等比数列前n项和公式就是用这种方法推导出来的),但要注意应按以上三种情况进行讨论,最后再综合成两种情况。
三、倒序相加
这是推导等差数列的前n项和公式时所用的方法,就是将一个数列倒过来排列(反序),再把它与原数列相加,就可以得到n个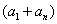 。
。
[例5] 求证: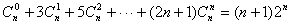
证明: 设 ………………………….. ①
………………………….. ①
把①式右边倒转过来得
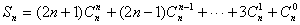 (反序)
(反序)
又由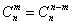 可得
可得
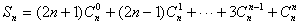 …………..…….. ②
…………..…….. ②
①+②得 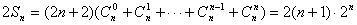 (反序相加)
(反序相加)
∴ 
解析:此类型关键是抓住数列中与首末两端等距离的两项之和相等这一特点来进行倒序相加的。
四、分组求和
有一类数列,既不是等差数列,也不是等比数列,若将这类数列适当拆开,可分为几个等差、等比或常见的数列,然后分别求和,再将其合并即可。
例:Sn=-1+3-5+7-…+(-1)n(2n-1)
解法:按n为奇偶数进行分组,连续两项为一组。
当n为奇数时:
 Sn=(-1+3)+(-5+7)+(-9+11)+…+(-2n+1)=2×
Sn=(-1+3)+(-5+7)+(-9+11)+…+(-2n+1)=2×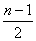 +(-2n+1)=-n
+(-2n+1)=-n
当n为偶数时:
Sn=(-1+3)+(-5+7)+(-9+11)+…+[(-2n+3)+(2n+1)] =2×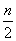 =n ∴Sn=
=n ∴Sn=
五、裂项法求和
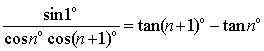 这是分解与组合思想在数列求和中的具体应用。 裂项法的实质是将数列中的每项(通项)分解,然后重新组合,使之能消去一些项,最终达到求和的目的通项分解(裂项)如:
这是分解与组合思想在数列求和中的具体应用。 裂项法的实质是将数列中的每项(通项)分解,然后重新组合,使之能消去一些项,最终达到求和的目的通项分解(裂项)如:
(1)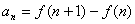 (2)
(2)
(3) (4)
(4)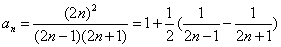
(5)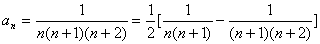
(6) 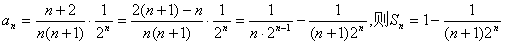
例:求数列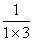 ,
,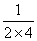 ,
,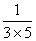 ,…,
,…,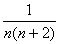 ,…的前n项和S
,…的前n项和S
解:∵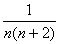 =
=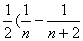 )
)
Sn=
=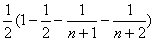
=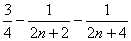
解析:要先观察通项类型,在裂项求和,而且要注意剩下首尾两项,还是剩下象上例中的四项,后面还很可能和极限、求参数的最大小值联系。
六、合并求和
针对一些特殊的数列,将某些项合并在一起就具有某种特殊的性质,因此,在求数列的和时,可将这些项放在一起先求和,然后再求Sn.
例: 数列{an}: ,求S2002.
,求S2002.
解:设S2002=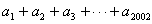 由
由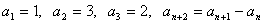 可得
可得
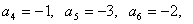
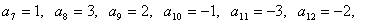
……
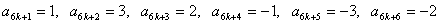
∵  (找特殊性质项)
(找特殊性质项)
∴ S2002=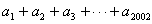 (合并求和)
(合并求和)
=
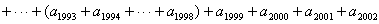
=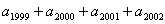 =
= =5
=5
七、拆项求和
先研究通项,通项可以分解成几个等差或等比数列的和或差的形式,再代入公式求和。
 例:求数5,55,555,…, 55 …5 的前n项和S n
例:求数5,55,555,…, 55 …5 的前n项和S n  解: 因为 55 …5=
解: 因为 55 …5= 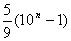
 所以 S n=5+55+555+…+ 55 …5
所以 S n=5+55+555+…+ 55 …5 =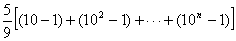 =
= =
=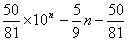
解析:根据通项的特点,通项可以拆成两项或三项的常见数列,然后再分别求和。
另外:Sn= 可以拆成:Sn=(1+2+3+…+n)+(
可以拆成:Sn=(1+2+3+…+n)+(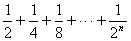 )
)
课堂小结:以上各种方法虽然各有其特点,但总的原则是要善于改变原数列的形式结构,使其能进行消项处理或能使用等差数列或等比数列的求和公式以及其它已知的基本求和公式来解决,只要很好地把握这一规律,就能使数列求和化难为易,迎刃而解.
课外作业:固学案相关习题
课后反思:
